Aspect physique¶

Définitions utiles dans le domaine du quadricoptère :¶

• Angle de calage : angle entre la corde et le plan de rotation de l'hélice
• Traînée : résistance de l'air sur l'hélice sur une hélice en rotation.
• Vitesse induite : vitesse communiquée à la molécule d'air lors de son passage au travers du disque rotor.

Terminologie¶

• Roll = Roulis
• Pitch = Tangage
• Yaw = Lacet

Effet à prendre en compte pour le vol d'un drone.¶

Cette partie relate des contraintes de l'environnement extérieur au drone et qui agisse dessus.

• L'effet de couple : Du fait que le l'hélice tourne dans un sens, le moteur tend à tourner dans le sens opposé en raison de la traînée induite par les pales. Il en résulte une légère inclinaison du moteur concerné. L'effet de couple dépend de la masse du l'hélice, de son pas, de son diamètre et de son régime, mais aussi et surtout à la puissance disponible : plus la puissance est grande, plus l'effet de couple est grand.
  L'inclinaison de l'axe du moteur en dû à l'effet de couple dépend de la résistance qui lui est opposé. Pour réduire cet effet, on peut appliquer deux types de « contre-mesures » :
  - les mesures passives qui ont lieu lors de la conception.
  - les mesures actives qui sont celle que l'on peut induire durant le vol (comme le report de poids d'un côté ou de l'autre, un réglage asymétrique du Trim, une réduction de poussée...).

• La précession gyroscopique : Une hélice qui tourne agit comme un gyroscope, qui initialement tend à résister à toute force qui pourrait lui faire changer d'axe de rotation.

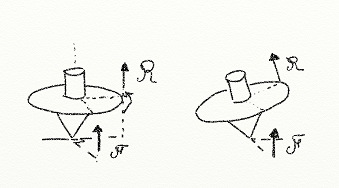
F la force instantanée appliquée au système en rotation, et R la résultante à 90 degrés dans le sens de rotation que le système va réellement "ressentir".

• La poussée asymétrique des pales : celle-ci a trois facteurs qui sont :
  - Elle se manifeste lorsque l'hélice n'est pas dans le plan horizontal, chacune des pales lorsqu'elle descend est entraînée vers l'avant, et lorsqu'elle monte vers l'arrière (phénomène dû bien entendu à la force de pesanteur).
  D'où en descente : vitesse air = vitesse sol + vitesse de rotation + vitesse d'entraînement.
  Et en montée : vitesse air = vitesse sol + vitesse de rotation – vitesse d'entraînement.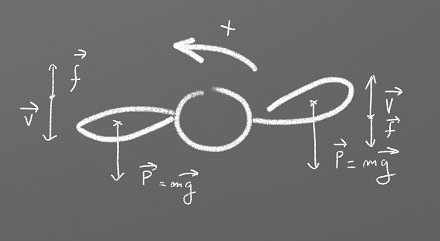
  
  Le poids de la pale P vient dans un cas s'additionner à la trainé f, et dans l'autre cas s'en soustraire. Il y a donc asymétrie dès lors que le drone n'est pas à l'horizontal.
  - Du fait de l'inclinaison du moteur, l'angle d'attaque de chaque pale est plus élevé dans la phase de descente que dans la phase de montée. Cela provoque plus de poussée d'un côté de l'hélice que de l'autre.
  - Les deux facteurs précédents induisent le fait que le côté où la pale descend est exposée à un flux d'air dit « propre » alors que l'autre subit un masquage aggravant. Cela provoque une poussée accrue du coté de descente, et réduit de l'autre, ce qui s'ajoute encore aux facteurs précédents, et on a donc une boucle.

A noter que la principale différence entre la précession gyroscopique et la poussée asymétrique des pales est que la première est une force momentanée qui disparaît dès le prochain changement d'assiette ; alors que la seconde est à peu de chose près permanente, de sorte que la direction réelle de l'appareil est toujours décalée par rapport à la direction souhaitée.

Il est également intéressant de noter que la poussée asymétrique des pales et la précession gyroscopique sont rapidement contrariées par une réduction de puissance et par l'évitement de changement d'assiette trop brut.

Analyse mécanique¶

Afin de déterminer quelles sont les contraintes internes au quadricoptère, il nous a fallu réaliser une analyse mécanique, et déterminer, si ces contraintes engendrent des problèmes, si une approche mécanique (classique) pouvait les paliers.

Théorie de l'élément de la pale (Froude)¶

La théorie de l'élément de la pale a été initialement développée par Froude qui assimile dans cette théorie l'élément de la pale à une plaque mince, soumise à un vent relatif. Cette théorie a été améliorée depuis par Drzewiecki qui calcule les caractéristiques aérodynamiques des hélices.

La pale est ici découpée en un nombre fini de tranches (éléments) à l'aide de surfaces cylindrique.

On suppose que l'écoulement dans un anneau, limité par deux surfaces voisines, est indépendant de l'écoulement dans les autres anneaux. Il est ainsi possible d'obtenir de façon indépendante les forces de traînée dD, et les forces de portance dL appliquée sur chaque tranche, sans tenir compte de l'écoulement dans les éléments voisins.

Enfin, en intégrant les efforts élémentaires, on peut calculer es caractéristique aérodynamique intégrales du rotor.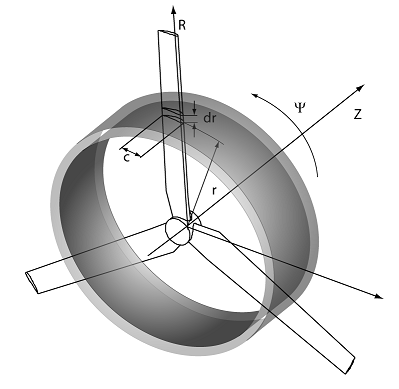

Pour obtenir l'effort élémentaire, chaque élément de la pale est donc représenté comme une aile cylindrique (aile à allongement infini), avec une surface dS = c*dr.
L'aile est soumise au vent résultant W, qui est une composition de la vitesse du vent à l'infini Vinf et celle de rotation U = Ωr.

W = √(Vinfini² + Ω²r²)    , c’est la vitesse relative en m/s (pas le travail)

Vinfini est la vitesse à l’amont en m/s.
Ω = vitesse angulaire en rad /r.
r = rayon local, correspond au r sur le schéma précédent

L'angle d'incidence α est calculé à partir de l'angle d'écoulement φ = arctan(Vinf / U), et l'angle de calage de la pale β : α =(φ-β).
La portance et la traînée peuvent maintenant être calculées à partir des formules :

dL=½ .ρ .W^2."CL" .α .c .dr
dS= ½ .ρ .W² ."CD" .α .c .dr

Où CL et CD sont les coefficients, respectivement, de traînée et de portance du profil d'aile.

Les valeurs de ces coefficients dépendent de l'angle d'incidence entre la corde du profil et la vitesse résultante. De façon générale, ces coefficients sont obtenus à partir d'essais de profils ou des simulations numériques prenant en compte la viscosité du milieu ; dans notre cas la méthode de recherche des coefficients par essais nous a semblé être plus facilement réalisable que la seconde méthode, qui nécessiterait des moyens d'envergures à son application.

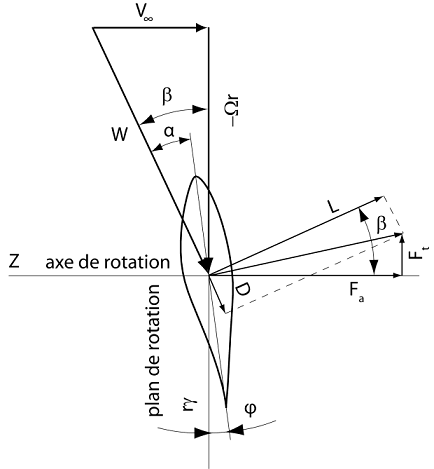
Afin d'obtenir la force tangentielle et la force axiale, appliquée à chaque élément de la pale, on projette les forces de traînée et de portance sur le plan de rotation et sur l'axe de rotation :

dFa = ½ .ρ .W² .[ "CL" .α .cos β + "CD" .α .sin β ] .c .r .dr 
dFt= ½ .ρ .W² .[ "CL" .α .sin β - "CD" .α .cos β ] .c .r .dr 

Finalement l'intégration de ces forces le long de la pale, du pied à l'extrémité permet d'obtenir la force axiale et la puissance du rotor.
En prenant en compte le nombre de pale N et la vitesse angulaire du rotor Ω, on obtient la force axiale Fa et la poussée P (en Watts) :

Fa = ½ .ρ . N .∫ [rp,R] ( W² .[ "CL" .α .cos β + "CD" .α .sin β ] .c .r .dr )
P = ½ .ρ .N .∫ [rp,R] ( W² .[ "CL" .α .sin β - "CD" .α .cos β ] .c .r .dr )

La théorie de l'élément de la pale donne des résultats satisfaisant à condition que les vitesses induites soient faibles.
h3.
Théorie de l'hélice

Comme la théorie de l'élément de la pale ne nous convient pas totalement nous nous sommes alors penchés sur la théorie de l'hélice, plus générale, et qui ne prend pas en compte le profil des pales.
Soient (i) l'angle d'incidence de la pale, (θ) l'angle de pas et (β) l'angle de conicité.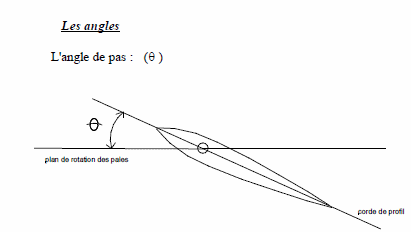

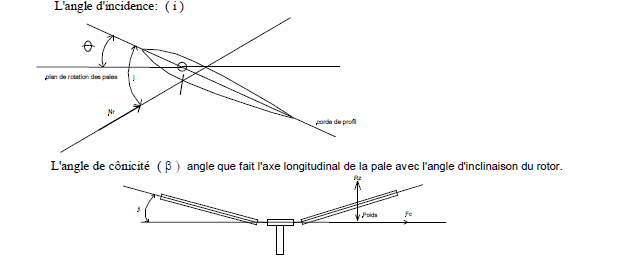
Plus l'angle d'incidence augmente, plus ρ us la portance augmente, jusqu'à une valeur limite où le profil décroche. Au décrochage, la portance s'écroule et la traînée croît brutalement.
La vitesse en chaque point de la pale augment proportionnellement à l'éloignement de l'axe de rotation, et la portance croît en fonction du carré de la vitesse.
La vitesse de rotation de la pale vaut : ωR, V est la vitesse de la pale et Vt la vitesse de translation.

La résultante aérodynamique en hauteur Rz est : Rz =  ½ . ρ . S . V² . CZ . ẑ

ρ = masse volumique du fluide du milieu en Kg/m3
S = maître couple en m²
V = vitesse en m/s
CZ = coefficient portance

Conclusion de l'analyse¶

Dans le cadre de notre projet, nous avons préféré substitué la résolution mécanique de l'instabilité du drone par une résolution mathématique utilisant un asservissement PID.

Ce choix est dû à la quantité de traitement qu'il n'est pas possible de réaliser avec le matériel présent sur le drone ou avec le budget qu'il nous est fourni. De plus la complexité des équations demanderait trop de temps pour pouvoir avoir un vol stabilisé dans les délais impartis.

Dans la prochaine partie nous aborderons donc la solution de stabilisation par PID que nous avons implémenté de façon concrète, et nous étudierons également la recherche des coefficients nécessaires à sa mise en place.

Dernière mise à jour : 27/03/2013 10h13
Auteur : Benjamin RIVRAY